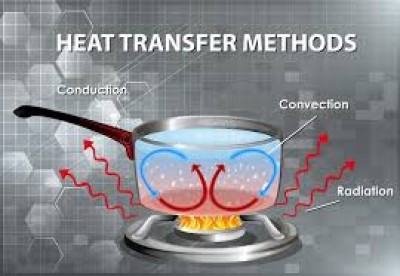
Conduction and Radiation
Overview Contents: Introduction, radiation from a black body: Introduction to three modes of heat transfer- conduction, convection and radiation. Importance of radiation, Mechanism of radiation,Electromagnetic spectrum. Concept of black body, derivation of black body radiation laws from first principles Planck's law, Stefan Boltzmann law, Wien's displacement law. Universal black body function, F function charts.
English
Last updated
Mon, 22-Aug-2022